ВЫБОРКИ ОБЪЕМ

число элементов, включенных в совокупность выборочную. В. о. определяется: а) задачами исследования; б) степенью однородности совокупности генеральной, которую данная выборка репрезентирует; в) величиной доверительной вероятности
(Р), при которой гарантируется достоверность результата исследований; д) требуемой точностью результатов, т. е. величиной допускаемой ошибки репрезентативности. При выборе В. о. учитывается совокупность технических приемов, применяемых для
ее качественного и статистического анализа. В. о. определяется с помощью статистических таблиц больших чисел, по номограммам достаточно больших чисел, а также с помощью специальных расчетов.
В тех случаях, когда отсутствует информация о средних показателях и дисперсии в выборочной и генеральной совокупностях, прибегают к таблицам достаточно больших чисел. В. о. зависит от вероятности (Р) заключения о достоверности выводов, от величины
предельной ошибки репрезентативности , а также от вероятности появления события (р). Практически достаточная величина Р не превышает 95 % (0,95). Допустимая ошибка репрезентативности,
т. е. погрешность производимых наблюдений, вычисляемая как доля от выборочной средней х, задается в пределах от 0,01 до 0,05. Чем выше величина доверительной вероятности Р и чем меньше допустимая ошибка репрезентативности, тем большим должно
быть число наблюдений (п).
Если средние показатели и дисперсия для выборочной и генеральной совокупностей известны, для определения В. о. можно воспользоваться специальным расчетом. При этом вначале определяется желательный уровень точности измерения, выражаемый в долях
измеряемой величины или процентах доверительной вероятности, напр.  или . Для непрерывно изменяющейся нормально распределенной
величины объем выборки (n) будет определяться по формуле:

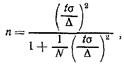
где N – объем генеральной совокупности, t – значение абсциссы для кривой нормального распределения, определяемое желательной точностью оценки или выбора (для P=0,95,  t = 1,96, для P=0,99, t=2,58), -уровень
точности в долях от  выборки,
- стандарное отклонение .
В качестве примера определим величину выборки для генеральной совокупности 5 тыс. человек: = 10, заданная ошибка не превышает 5% от среднего значения, вероятность попадания значений
переменной за пределы доверительного интервала  не более 5% (Р=0,95), стандартное отклонение =2;

 
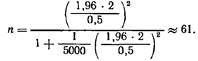
Как видно из расчетной формулы В. о., при заданной предельной ошибке с возрастанием дисперсии признака и надежности заключения, выражаемой вероятностью Р, число наблюдений в выборке увеличивается.