Меры изменчивости
Меры изменчивости
статистические показатели вариации (разброса) значений признака (переменной) относительно среднего значения, степени отклонения индивидуальных показателей от центральной тенденции распределения. М. и. позволяют судить о достоверности и однородности эмпирически полученной совокупности данных, существенности сходств и различий в распределении и сравниваемых группах распределений, точности проведенных измерений.
Источник: Основные понятия психодиагностики и экспериментальной психологии. Cловарь 2006
МЕРЫ ИЗМЕНЧИВОСТИ
статистические показатели вариации (разброса) признака (переменной) относительно среднего значения, степени индивидуальных отклонений от центральной тенденции распределения. М. и. позволяют судить о достоверности и однородности
полученной эмпирически совокупности данных, существенности сходств и различий в распределении и сравниваемых группах распределений, точности проведенных измерений.
Одна и та же средняя величина может характеризовать совокупности данных, в которых размеры вариации признака значительно отличаются друг от друга. Так, напр., при обследовании уровня достижений по отдельному предмету двух групп учащихся может
оказаться, что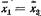 однако в первой группе показатели достижений плотно концентрируются около
однако в первой группе показатели достижений плотно концентрируются около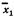 , что отражает одинаковый,
, что отражает одинаковый,
стабильный уровень подготовки, а зо второй — наблюдается значительный разброс (часть учащихся, предположим, в силу индивидуальных интересов и самостоятельной углубленной подготовки достигают очень хороших результатов, в то время как большинство
других имеют показатели существенно ниже, чем в первой группе).
Наиболее простым и наглядным способом представления разброса данных является размах распределения, т. е. разность между самым высоким а самым низким результатом. Однако эта М. и. неточна и неустойчива, поскольку характеризует только два показателя
в выборке независимо от объема последней. Случайный необычно низкий или высокий результат может заметно повлиять на величину размаха. Более точная М. и. основана на учете разности между каждым индивидуальным результатом и средним значением
по группе. Таким показателем является среднее абсолютное (линейное, арифметическое) отклонение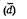
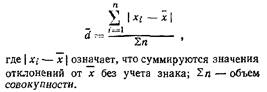
Недостаток показателя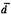 заключается в том, что он не учтывает знак отклонения, поэтому гораздо более информативными М.и. являются дисперсия и среднеквадратическое отклонение.
заключается в том, что он не учтывает знак отклонения, поэтому гораздо более информативными М.и. являются дисперсия и среднеквадратическое отклонение.
Дисперсия представляет собой среднюю квадрата отклонений индивидуальных значений признака от их средней величины и обозначается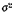 :
:
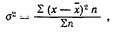
где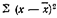 сумма квадратов разностей между средним и индивидуальным значением признака; n - количество вариантов.
сумма квадратов разностей между средним и индивидуальным значением признака; n - количество вариантов.
Расчет дисперсий применяют для выделения выборочной совокупности, определения ошибки выборки, однородности изучаемой совокупности по тому или иному признаку. Он лежит в основе факторного анализа, дисперсионного анализа и ряда других статистических
методов.
Применение дисперсии, как М. и., не всегда удобно, т. к. размерность дисперсии равна квадрату размерности изучаемого признака. Поэтому для измерения вариаций вычисляется среднее квадратическое отклонение а, равное корню квадратному из суммы квадратов
отклонений индивидуальных значений признака от среднего, т. е. дисперсии
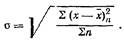
Следует заметить, что более точной характеристикой дисперсии является величина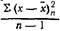 . Такая поправка необходима при небольших статистических выборках.
. Такая поправка необходима при небольших статистических выборках.
Величина квадратного корня из дисперсии носит также название стандартного отклонения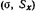 . Стандартное отклонение является общеупотребимой мерой вариации, так как для многих распределений,
. Стандартное отклонение является общеупотребимой мерой вариации, так как для многих распределений,
приближающихся к нормальному, мы приблизительно знаем, какой процент данных лежит внутри одного, двух, трех и более стандартных отклонений от среднего.
Дисперсия и среднее квадратическое отклонение как меры вариации признака имеют некоторые недостатки. Они недостаточно точно характеризуют изменчивость признака, т. к. отражают абсолютный размер отклонений. Это неудобно при сопоставлении распределений
с различными размерностью и значением признаков. Для устранения этого недостатка абсолютные числа переводятся в относительные. Отношение квадратического отклонения к средней, выраженное в процентах, называется коэффициентом вариации V
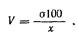
Отношение среднего линейного отклонения к средней арифметической, выраженное в процентах, называется линейным коэффициентом вариации
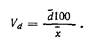
Отношение размаха вариации (R) в средней арифметической, выраженное в процентах, называется коэффициентом асцилляции
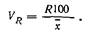
полученной эмпирически совокупности данных, существенности сходств и различий в распределении и сравниваемых группах распределений, точности проведенных измерений.
Одна и та же средняя величина может характеризовать совокупности данных, в которых размеры вариации признака значительно отличаются друг от друга. Так, напр., при обследовании уровня достижений по отдельному предмету двух групп учащихся может
оказаться, что
стабильный уровень подготовки, а зо второй — наблюдается значительный разброс (часть учащихся, предположим, в силу индивидуальных интересов и самостоятельной углубленной подготовки достигают очень хороших результатов, в то время как большинство
других имеют показатели существенно ниже, чем в первой группе).
Наиболее простым и наглядным способом представления разброса данных является размах распределения, т. е. разность между самым высоким а самым низким результатом. Однако эта М. и. неточна и неустойчива, поскольку характеризует только два показателя
в выборке независимо от объема последней. Случайный необычно низкий или высокий результат может заметно повлиять на величину размаха. Более точная М. и. основана на учете разности между каждым индивидуальным результатом и средним значением
по группе. Таким показателем является среднее абсолютное (линейное, арифметическое) отклонение
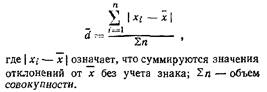
Недостаток показателя
Дисперсия представляет собой среднюю квадрата отклонений индивидуальных значений признака от их средней величины и обозначается
где
Расчет дисперсий применяют для выделения выборочной совокупности, определения ошибки выборки, однородности изучаемой совокупности по тому или иному признаку. Он лежит в основе факторного анализа, дисперсионного анализа и ряда других статистических
методов.
Применение дисперсии, как М. и., не всегда удобно, т. к. размерность дисперсии равна квадрату размерности изучаемого признака. Поэтому для измерения вариаций вычисляется среднее квадратическое отклонение а, равное корню квадратному из суммы квадратов
отклонений индивидуальных значений признака от среднего, т. е. дисперсии
Следует заметить, что более точной характеристикой дисперсии является величина
Величина квадратного корня из дисперсии носит также название стандартного отклонения
приближающихся к нормальному, мы приблизительно знаем, какой процент данных лежит внутри одного, двух, трех и более стандартных отклонений от среднего.
Дисперсия и среднее квадратическое отклонение как меры вариации признака имеют некоторые недостатки. Они недостаточно точно характеризуют изменчивость признака, т. к. отражают абсолютный размер отклонений. Это неудобно при сопоставлении распределений
с различными размерностью и значением признаков. Для устранения этого недостатка абсолютные числа переводятся в относительные. Отношение квадратического отклонения к средней, выраженное в процентах, называется коэффициентом вариации V
Отношение среднего линейного отклонения к средней арифметической, выраженное в процентах, называется линейным коэффициентом вариации
Отношение размаха вариации (R) в средней арифметической, выраженное в процентах, называется коэффициентом асцилляции
Источник: Словарь-справочник по психологической диагностике 1989 г.